Quanto mede a circunferância da Terra ?

Há anos antes de Cristo já se sabia o comprimento da circunferância do planeta Terra. ERATÓSTENES viveu no Egito entre os anos 276 E 194 antes de Cristo. Ele era bibliotecário-chefe da famosa Biblioteca de Alexandria, e foi lá que encontrou, num velho papiro, indicações de que ao meio-dia de cada 21 de junho na cidade de Siena, 800 km ao sul de Alexandria, uma vareta fincada verticalmente no solo não produzia sombra. Informação inútil, diriam alguns. Não para um homem observador como Eratóstenes. Ele percebeu que o mesmo fenômeno não ocorria no mesmo dia e horário em Alexandria. Sendo assim ele parou e pensou:


Se o mundo é plano como uma mesa, então as sombras das varetas têm de ser iguais. Se isto não acontece é porque a Terra deve ser curva! E ficou encabulado com isso, até mostrar e provar que a terra então é curva, e que formaria uma circunferância.
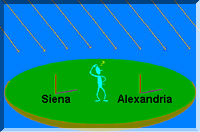
Varetas fincadas verticalmente no chão em lugares diferentes lançariam sombras de comprimentos distintos. Eratóstenes decidiu fazer um experimento. Ele mediu o comprimento da sombra em Alexandria ao meio-dia de 21 de junho, quando a vareta em Siena não produzia sombra. Assim obteve o ângulo A, conforme a figura abaixo.

Eratóstenes mediu A=7° (aproximadamente). Se as varetas estão na vertical, dá para imaginar que se fossem longas o bastante iriam se encontrar no centro da Terra. Preste atenção na figura acima. O ângulo B terá o mesmo valor que A, pois o desenho de Eratóstenes se reduz a uma geometria muito simples: se duas retas paralelas interceptam uma reta transversal, então os ângulos correspondentes são iguais.

As retas paralelas são os raios de luz do Sol e a reta transversal é a que passa pelo centro da Terra e pela vareta em Alexandria. O ângulo B (também igual a 7°), é a uma fração conhecida da circunferência da Terra e corresponde à distância entre Siena e Alexandria!
Sendo assim, Eratóstenes pensou: Se 7º equivale a 800 km (distância entre Alexandria e Siena), 360º equivale a quanto? Logo a circunferância da Terra mede aproximadamente 40.075 km !

Fonte: http://www.zenite.nu/